Sight Distance in Highway Engineering – Types and Calculations
The visibility of the road ahead of the driver will help in the safe and efficient operation of the vehicles. This will hence demand the geometric design to be highly efficient so that the length of the road is highly visible to the driver even from a distance ahead. This distance is hence termed as the sight distance.
Sight Distance and Their Types
The actual distance that is observed along the road surface which is visible for a driver from a specified height above the carriage way is called as the sight distance at a point. This distance will let the driver see all the stationary and the moving objects in front of the vehicle.
Mainly in the geometric design of road construction, mainly three sight distances are taken into consideration. They are:
- SSD – Stopping Sight Distance or Absolute Minimum Sight Distance
- ISD – Intermediate Sight Distance: This is twice the value of SSD
- OSD – Overtaking Sight Distance
Other than these we have:
- Head Light Sight Distance
- Safe Sight Distance
The distance that is available for the driver during the night travel is called as the head light sight distance. At night the drive is facilitated by the illumination of the head lights.
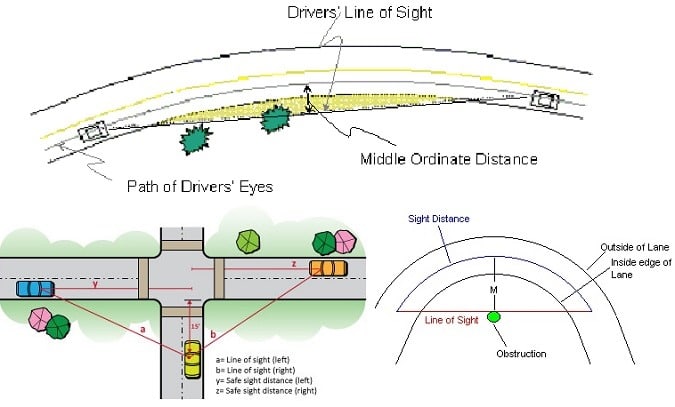
The sight distance available to enter an intersection is called as the Safe sight distance.
Whatever be the stopping distance taken into consideration, it is necessary for the driver who is traveling at the design speed to possess sufficient carriage way distance. This distance will be within the line of vision to stop the vehicle from colliding with a moving or stationary object in the traffic lane.
Stopping Sight Distance
This is defined as the sight distance that is available for the moving the vehicle in the highway that will enable the driver to stop the vehicle safely without collision with any other obstacle.
As mentioned above, the parameter safe stopping distance is the most important feature in the traffic engineering. Safe stopping distance is the distance from the point it first perceives to the time the deceleration is complete. Adequate time is necessary for the drivers for them to react to the obstacle spontaneously.
This demand the sight distance used in the geometric design to be equal to the safe stopping distance. The Stopping distance can be defined as the sum of Lagging distance to the brake distance.
The lagging distance is the distance that is moved by the vehicle in a time period ‘t’ at a velocity of ‘v’ in m/s. Hence lag distance is ‘vt’.
The distance that is traveled by the vehicle during the operation of braking is called as the braking distance. In the case of a level road, the work that is done in stopping the vehicle is equated to the kinetic energy of the vehicle which will give us the braking distance.
Let ‘F’ be the maximum frictional force that is developed and ‘l’ be the braking distance. Hence, the work that is done against friction is given by
Fl = fWl –> (1)
Here W = the weight of the vehicle. The Kinetic energy attained at the design speed of the vehicle
= (1/2g) mv2 = (1/2g)Wv2 –> (2)
(1) Is equated to (2), we get
(1/2g) Wv2 = fWl
l = (1/(2fg))v2
Hence,
The Stopping Sight Distance (SSD) = Lag Distance + Braking Distance
-> SSD = vt + (1/(2fg))v2
Here, v is the speed in m/s2, t is the reaction time taken, f is coefficient of friction, g is the acceleration due to gravity.
The Table-1 Below shows the coefficient of friction for different design speeds.
Table-1: Coefficient of longitudinal friction
| Speed kmph | <0 | 40 | 50 | 60 | >80 |
| f | 0.4 | 0.38 | 0.37 | 0.36 | 0.5 |
If the road possesses an ascending gradient in an amount equal to +n%, to the braking action the component factor of gravity will be added. This will decrease the braking distance. This component of gravity is acting along the direction of the braking force which is given by
Wsin? ~ Wtan? = Wn/100
After equating the kinetic energy and the work done we get,
l = v2 / (2g (f + n/100 ))
We can also derive the braking distance for a descending gradient which is performed similarly, and we get:
SSD = vt + (v2/ (2g (f ±0.01n)))
Overtaking Sight Distance (OSD)

Fig.1: Representing Overtaking Sight Distance through Time Space Diagram
The minimum distance available for the driver to safely overtake the slow vehicle in front of him by considering the traffic in the opposite direction is called as the overtaking sight distance. This distance will make us see whether the road is clear to undergo an overtaking movement.
The overtaking sight distance is also called as the passing sight distance that will be measured along the center line of the road. This is the line level over which the driver keeping an eye level of 1.2 m above the road level can easily see the top of the object 1.2 m above the road surface.
Factors Affecting Overtaking Sight Distance
The main factors that affect the OSD are:
- Spacing Between the vehicles
- Speed of the vehicles
- The gradient of the road
- The acceleration rate of the overtaking vehicle
- The velocities of the vehicle which is overtaking, overtaken and that coming in the opposite direction
- The driver skill
- The reaction of the driver
Computation of Sight Distance
The computation of the sight distance mainly depends on the:
- Driver’s Reaction Time
- Vehicle’s Speed
- Efficiency of Brakes
- The frictional Resistance Existing Between the Tire and Road
- Gradient of Road
Brake Efficiency
Many factors like the age of the vehicle, the characteristics of the vehicle will affect the brake efficiency of the vehicle. An efficiency of 100% implies that the vehicle will stop at the moment the brake is applied. Obtaining 100% is not practicable. This is an ideal condition of the vehicle.
This means, for a lower value of brake efficiency, it is necessary to obtain a higher value of sight distance. In the process of determining a safe geometric design, it is required to assume 50% brake efficiency.
Friction between the Road and the Tire
The stopping of a vehicle is also dependent on the frictional resistance between the tire and the road. Having a higher value of frictional resistance will result in efficient stopping of the vehicle when applied. Here, the sight distance required will be less.
During the computation of sight distance, no special provision or consideration is given for the brake efficiency. This is considered along with the factor of longitudinal friction. In India, the value of longitudinal friction is between 0.35 and 0.4. This is as per the Indian Road Congress.
Speed of the Vehicle
The speed of the vehicle clearly affects the sight distance. If the speed employed is high, the time required to stop the vehicle will be high. This means that with the increase in the speed there is increase in the sight distance.
Driver’s Reaction Time
The time from the moment the driver observes the obstacle in front of him to the moment he applies brake is called as the reaction time of the driver. Based on the PIEV theory, the reaction time can be divided into 4 components.
All these times will be combined to form a total perception reaction time while undergoing actual practice and design of highway. From studies conducted it is reviewed that the drivers will require about 1.5 to 2 seconds for normal conditions. As this value may vary based on the characteristics of the vehicle, a higher value for the reaction time can be employed for the design purpose. In India, as per IRC, the reaction time is set to be 2.5 seconds.
Gradient of Road
The sight distance is greatly influenced by the gradient of the road. There are chances for the vehicles to stop suddenly when the vehicle is climbing suddenly. This situation will ask for a small sight distance. When the vehicle is moving down, the movement is supported by the gravity action. This will hence ask for more time to stop the vehicle. In this situation, the required sight distance is more.

No comments:
Post a Comment